39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 4: resolução
Numa reação química, há o envolvimento entre elétrons e núcleos atômicos eletrizados. Portanto, trata-se de uma manifestação de força eletromagnética.
Resposta: c
Clique aqui para voltar ao Blog
quarta-feira, 23 de dezembro de 2015
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 3: resolução
0: verdadeira
A força de interação entre massas é a força gravitacional
1: verdadeira
A força eletromagnética é a que existe entre partículas eletrizadas, englobando as forças elétricas e as forças magnéticas.
2: verdadeira
A força nuclear forte mantém a coesão do núcleo atômico e garante a união dos quarks para formarem os prótons e os nêutrons, assim como a ligação dos prótons entre si, equilibrando a força eletrostática repulsiva entre cargas de mesmo sinal.
3: Falsa
A força nuclear fraca tem intensidade menor que a força eletromagnética.
4: verdadeira
A força gravitacional é a menos intensa das quatro forças.
Verdadeiras (coluna I): 0, 1, 2 e 4
Falsa (coluna II): 3
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 3: resolução
0: verdadeira
A força de interação entre massas é a força gravitacional
1: verdadeira
A força eletromagnética é a que existe entre partículas eletrizadas, englobando as forças elétricas e as forças magnéticas.
2: verdadeira
A força nuclear forte mantém a coesão do núcleo atômico e garante a união dos quarks para formarem os prótons e os nêutrons, assim como a ligação dos prótons entre si, equilibrando a força eletrostática repulsiva entre cargas de mesmo sinal.
3: Falsa
A força nuclear fraca tem intensidade menor que a força eletromagnética.
4: verdadeira
A força gravitacional é a menos intensa das quatro forças.
Verdadeiras (coluna I): 0, 1, 2 e 4
Falsa (coluna II): 3
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 2: resolução
As nomenclaturas das quatro forças fundamentais da natureza, omitidas no texto são:
i) força nuclear forte,
ii) força nuclear fraca,
iii) força eletromagnética,
iv) força gravitacional.
Resposta: c
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 2: resolução
As nomenclaturas das quatro forças fundamentais da natureza, omitidas no texto são:
i) força nuclear forte,
ii) força nuclear fraca,
iii) força eletromagnética,
iv) força gravitacional.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 1: resolução
A força normal e a força de tração são de origem eletromagnética.
Resposta: c
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 1: resolução
A força normal e a força de tração são de origem eletromagnética.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 5: resolução
Numa reação química há o envolvimento entre os elétrons e os núcleos atômicos eletrizados. Portanto, trata-se de uma manifestação de forças eletromagnéticas.
Resposta: c
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 5: resolução
Numa reação química há o envolvimento entre os elétrons e os núcleos atômicos eletrizados. Portanto, trata-se de uma manifestação de forças eletromagnéticas.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 4: resolução
Resposta: a
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 4: resolução
Resposta: a
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 3: resolução
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 3: resolução
Coluna I: 0, 1, 2 e 4, verdadeiras; Coluna II: 3, falsa
x
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 2: resolução
Resposta:
B => I
C => I
D => II
A => IV
x
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 2: resolução
Resposta:
B => I
C => I
D => II
A => IV
x
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 1: resolução
A força de atrito e a força normal resultam da interação entre partículas eletrizadas próximas. São, portanto, forças eletromagnéticas.
Resposta: c
x
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 1: resolução
A força de atrito e a força normal resultam da interação entre partículas eletrizadas próximas. São, portanto, forças eletromagnéticas.
Resposta: c
x
Clique aqui para voltar ao Blog
terça-feira, 22 de dezembro de 2015
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 5: resolução
f = v/4L => f = 340/4.2,5.10-2 => f = 3,4.103 Hz
Resposta: 3,4.103 Hz
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Revisão/Ex 4: resolução
fSol = (4/5).fSi => vSol/2L = (4/5).vSi/2L => vSol = (4/5).vSi =>
√(fSol/μ) = (4/5)√(fSi/μ) =>
fSol = (16/25).fSi
Resposta: b
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 3: resolução
fM = 2.fm => vM/2L = 2.vm/2L => vM = 2.vm =>
√(F/μM) = 2.√(F/μm) = μm/μM = 4
Resposta: b
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 2: resolução
A) Correta. A propagação do som não ocorre no vácuo, isto é, só ocorre em um meio material.
B) Correta. O maior comprimento de onda possível corresponde ao modo mais simples de a corda vibrar, isto é a um nó em cada extremidade e entre eles um único ventre.
Sendo L ao comprimento da corda, obtemos: L = λ/2 => λ = 2L
C) Correta. De v = √(F/μ) => v2 = F/(m/L) => v2 = F.L/m
D) Incorreta. No tubo sonoro fechado temos sempre um ventre na embocadura e um nó na outra extremidade. O modo mais simples de vibração é representado abaixo:
Temos: L = λ/4 => λ = 4L
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 1: resolução
a) Com a corda vibrando no seu modo fundamental, temos dois nós nas extremidades e um ventre. Logo,
λ/2 = L => λ/2 = 0,35 m => λ = 0,70 m
v = λ.f => v = 0,7.680 => v = 476 m/s
b) A frequência fundamental da onda sonora é a frequência fundamental de vibração da corda.
v = λ.f => 340 = λ.680 => λ = 0,50 m
Respostas; a) 476 m/s b) 0,50 m
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39° aula
Cordas vibrantes / Tubos sonoros
Borges e Nicolau
Exercícios básicos
Exercício 6: resolução
Clique aqui para voltar ao Blog
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 6: resolução
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 5: resolução
Tubo aberto:
Tubo fechado:
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 4: resolução
λ/4 + λ/2 + λ/2 = L => λ = 4.L/5 e f = 5.v/4.L
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 3: resolução
λ/4 + λ/2 + λ/2 + λ/4 = L => λ = 2.L/3 e f = 3.v/2.L
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 2: resolução
a)
b)
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 1: resolução
L = 3.λ/2; λ = 2.L/3; f = 3.(v/2L)
L = 4.λ/2; λ = 2.L/4; f = 4.(v/2L)
Clique aqui para voltar ao Blog
segunda-feira, 21 de dezembro de 2015
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 5: resolução
Tomando o ponto A como referência:
MPplaca + MPbarra = MT.senB => 200.8 + 100.4 = T.(6/10).8 =>
1600 + 400 = T.4,8 => T = 2000/4,8 => T = 416,66 N => T ≅ 417 N
Resposta: a
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 5: resolução
MPplaca + MPbarra = MT.senB => 200.8 + 100.4 = T.(6/10).8 =>
1600 + 400 = T.4,8 => T = 2000/4,8 => T = 416,66 N => T ≅ 417 N
Resposta: a
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
A máxima distância que o jovem pode percorrer, medida a partir de B, sem que a prancha gire, corresponde ao instante em que a força normal em A torna-se nula.
Nestas condições, tomando o ponto B como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Pprancha x 1,5 = Pjovem x d => 900 x 1,5 = 600 x d => d = 2,25 m
Resposta: c
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
A máxima distância que o jovem pode percorrer, medida a partir de B, sem que a prancha gire, corresponde ao instante em que a força normal em A torna-se nula.
Nestas condições, tomando o ponto B como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Pprancha x 1,5 = Pjovem x d => 900 x 1,5 = 600 x d => d = 2,25 m
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
mB.g.30 = mA.g.10 => mB = mA/3 = 15 gramas.
T = mA.g + mB.g = 60.g
T.20 = mC.g.30 => 60.g.20 = mC.g.30 => mC = 40 gramas
Resposta: d
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
mB.g.30 = mA.g.10 => mB = mA/3 = 15 gramas.
T = mA.g + mB.g = 60.g
T.20 = mC.g.30 => 60.g.20 = mC.g.30 => mC = 40 gramas
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
Tomando a articulação como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Mg.L + mg.(L/2) = Kx.(L/2) => x = (2M+m).g/K
Resposta: d
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
Tomando a articulação como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Mg.L + mg.(L/2) = Kx.(L/2) => x = (2M+m).g/K
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Tomando o ponto P como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Phaste.(L/2) + Mg.2L = M’g.L => M’ = 2M + Phaste/2g
Portanto, M’ > 2M
Resposta: d
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Tomando o ponto P como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Phaste.(L/2) + Mg.2L = M’g.L => M’ = 2M + Phaste/2g
Portanto, M’ > 2M
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 5: resolução
Condições de equilíbrio:
1ª) YA + T.sen 30º = P + PB => YA + T.(1/2) = 30 + 10 (1)
XA = T.cos 30º => XA = T.(√3/2) (2)
2ª) Tomando o ponto A como referência:
MP + MPB = MTsen30º => 30.3 + 10.6 = T.(1/2).4 => T = 75 N
De (1): YA = 2,5 N
De (2): XA = 37,5.√3 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 5: resolução
Condições de equilíbrio:
1ª) YA + T.sen 30º = P + PB => YA + T.(1/2) = 30 + 10 (1)
XA = T.cos 30º => XA = T.(√3/2) (2)
2ª) Tomando o ponto A como referência:
MP + MPB = MTsen30º => 30.3 + 10.6 = T.(1/2).4 => T = 75 N
De (1): YA = 2,5 N
De (2): XA = 37,5.√3 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
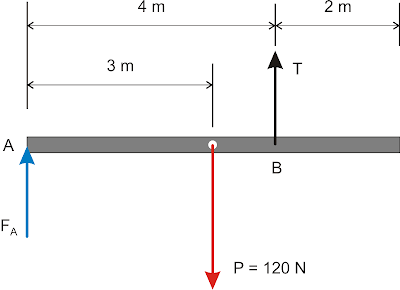
Exercício 4: resolução
Condições de equilíbrio:
1ª ) FA + T = P => FA + T = 120 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 120.3 = T.4 => T = 90 N
Mas o peso do bloco é igual à intensidade da força de tração no fio, isto é:
P = T = 90 N
De (1): FA = 30 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 4: resolução
Condições de equilíbrio:
1ª ) FA + T = P => FA + T = 120 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 120.3 = T.4 => T = 90 N
Mas o peso do bloco é igual à intensidade da força de tração no fio, isto é:
P = T = 90 N
De (1): FA = 30 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 3: resolução
Tomando o ponto O como referência:
MPJ = MPM => 500.2 = PM.4 => PM = 250 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 3: resolução
Tomando o ponto O como referência:
MPJ = MPM => 500.2 = PM.4 => PM = 250 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 2: resolução
a)
b) Condições de equilíbrio:
1ª) FA + T = P => FA + T = 90 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 90.2 = T.4 => T = 45 N
De (1): FA = 45 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 2: resolução
a)
b) Condições de equilíbrio:
1ª) FA + T = P => FA + T = 90 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 90.2 = T.4 => T = 45 N
De (1): FA = 45 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 1: resolução
a) MF = F.d = 10 N.2 m = 20 N.m
b) MFA = 0, pois a distância de A à linha de ação de fA é zero.
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 1: resolução
a) MF = F.d = 10 N.2 m = 20 N.m
b) MFA = 0, pois a distância de A à linha de ação de fA é zero.
Clique aqui para voltar ao Blog
quarta-feira, 16 de dezembro de 2015
Cursos do Blog - Eletricidade
38ª aula
O átomo de Bohr
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
De En = -13,6/n2 (eV), vem:
para n = 2: E’ = -3,4 eV para n = 1: E = -13,6 eV
A energia absorvida é igual a: ΔE: E’ – E = -3,4 eV-(-13,6 eV) = 10,2 eV
ΔE = h.f => 10,2 = 4,14.10-15.f => f ≅ 2,5.1015 Hz
v = λ.f => 3,0.108 = λ. 2,5.1015 => λ = 1,2.10-7 m
Pelo diagrama concluímos que a radiação correspondente a este comprimento de onda é o ultravioleta.
Resposta: c
Clique aqui para voltar ao Blog
O átomo de Bohr
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
De En = -13,6/n2 (eV), vem:
para n = 2: E’ = -3,4 eV para n = 1: E = -13,6 eV
A energia absorvida é igual a: ΔE: E’ – E = -3,4 eV-(-13,6 eV) = 10,2 eV
ΔE = h.f => 10,2 = 4,14.10-15.f => f ≅ 2,5.1015 Hz
v = λ.f => 3,0.108 = λ. 2,5.1015 => λ = 1,2.10-7 m
Pelo diagrama concluímos que a radiação correspondente a este comprimento de onda é o ultravioleta.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
38ª aula
O átomo de Bohr
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
De En = -13,6/n2 (eV), vem:
para n = 2: E’ = -3,4 eV para n = 1: E = -13,6 eV
A energia absorvida é igual a: ΔE = E’ – E = -3,4 eV-(-13,6 eV) = 10,2 eV
Resposta: b
Clique aqui para voltar ao Blog
O átomo de Bohr
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
De En = -13,6/n2 (eV), vem:
para n = 2: E’ = -3,4 eV para n = 1: E = -13,6 eV
A energia absorvida é igual a: ΔE = E’ – E = -3,4 eV-(-13,6 eV) = 10,2 eV
Resposta: b
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
38ª aula
O átomo de Bohr
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Para haver emissão de um fóton o elétron deve transitar de um nível de maior energia para outro de menor.
ΔE = h.f => ΔE = h.(c/λ) => λ = (h.c)/ΔE
O menor valor de λ corresponde ao maior valor de ΔE, correspondendo, portanto, à transição III.
Resposta: c
Clique aqui para voltar ao Blog
O átomo de Bohr
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Para haver emissão de um fóton o elétron deve transitar de um nível de maior energia para outro de menor.
ΔE = h.f => ΔE = h.(c/λ) => λ = (h.c)/ΔE
O menor valor de λ corresponde ao maior valor de ΔE, correspondendo, portanto, à transição III.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
38ª aula
O átomo de Bohr
Borges e Nicolau
a) A origem da radiação está relacionada com a passagem do elétron dos1níveis de energia: E3 para E1, E3 para E2 e E2 para E1 .
x
b) De c = λ.f notamos que ao menor valor de λ (que é λa) corresponde o maior valor de f.
De ΔE = h.f resulta que o maior valor de f corresponde ao maior valor de ΔE.1
Portanto ΔE = E3 - E1.
E3 - E1 = h.f => E3 - E1 = h.(c/λa) => λa = h.c/(E3 - E1)
x
Clique aqui para voltar ao Blog
O átomo de Bohr
Borges e Nicolau
Exercícios básicos
Exercício 3: resolução
a) A origem da radiação está relacionada com a passagem do elétron dos1níveis de energia: E3 para E1, E3 para E2 e E2 para E1 .
x
b) De c = λ.f notamos que ao menor valor de λ (que é λa) corresponde o maior valor de f.
De ΔE = h.f resulta que o maior valor de f corresponde ao maior valor de ΔE.1
Portanto ΔE = E3 - E1.
E3 - E1 = h.f => E3 - E1 = h.(c/λa) => λa = h.c/(E3 - E1)
x
Clique aqui para voltar ao Blog
Assinar:
Postagens (Atom)