39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 4: resolução
Numa reação química, há o envolvimento entre elétrons e núcleos atômicos eletrizados. Portanto, trata-se de uma manifestação de força eletromagnética.
Resposta: c
Clique aqui para voltar ao Blog
quinta-feira, 10 de dezembro de 2020
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 3: resolução
0: verdadeira
A força de interação entre massas é a força gravitacional
1: verdadeira
A força eletromagnética é a que existe entre partículas eletrizadas, englobando as forças elétricas e as forças magnéticas.
2: verdadeira
A força nuclear forte mantém a coesão do núcleo atômico e garante a união dos quarks para formarem os prótons e os nêutrons, assim como a ligação dos prótons entre si, equilibrando a força eletrostática repulsiva entre cargas de mesmo sinal.
3: Falsa
A força nuclear fraca tem intensidade menor que a força eletromagnética.
4: verdadeira
A força gravitacional é a menos intensa das quatro forças.
Verdadeiras (coluna I): 0, 1, 2 e 4
Falsa (coluna II): 3
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 3: resolução
0: verdadeira
A força de interação entre massas é a força gravitacional
1: verdadeira
A força eletromagnética é a que existe entre partículas eletrizadas, englobando as forças elétricas e as forças magnéticas.
2: verdadeira
A força nuclear forte mantém a coesão do núcleo atômico e garante a união dos quarks para formarem os prótons e os nêutrons, assim como a ligação dos prótons entre si, equilibrando a força eletrostática repulsiva entre cargas de mesmo sinal.
3: Falsa
A força nuclear fraca tem intensidade menor que a força eletromagnética.
4: verdadeira
A força gravitacional é a menos intensa das quatro forças.
Verdadeiras (coluna I): 0, 1, 2 e 4
Falsa (coluna II): 3
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 2: resolução
As nomenclaturas das quatro forças fundamentais da natureza, omitidas no texto são:
i) força nuclear forte,
ii) força nuclear fraca,
iii) força eletromagnética,
iv) força gravitacional.
Resposta: c
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 2: resolução
As nomenclaturas das quatro forças fundamentais da natureza, omitidas no texto são:
i) força nuclear forte,
ii) força nuclear fraca,
iii) força eletromagnética,
iv) força gravitacional.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 1: resolução
A força normal e a força de tração são de origem eletromagnética.
Resposta: c
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios de Revisão
Revisão/Ex 1: resolução
A força normal e a força de tração são de origem eletromagnética.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 5: resolução
Numa reação química há o envolvimento entre os elétrons e os núcleos atômicos eletrizados. Portanto, trata-se de uma manifestação de forças eletromagnéticas.
Resposta: c
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 5: resolução
Numa reação química há o envolvimento entre os elétrons e os núcleos atômicos eletrizados. Portanto, trata-se de uma manifestação de forças eletromagnéticas.
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 4: resolução
Resposta: a
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 4: resolução
Resposta: a
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 3: resolução
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 3: resolução
Coluna I: 0, 1, 2 e 4, verdadeiras; Coluna II: 3, falsa
x
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 2: resolução
Resposta:
B => I
C => I
D => II
A => IV
x
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 2: resolução
Resposta:
B => I
C => I
D => II
A => IV
x
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
39ª aula
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 1: resolução
A força de atrito e a força normal resultam da interação entre partículas eletrizadas próximas. São, portanto, forças eletromagnéticas.
Resposta: c
x
Clique aqui para voltar ao Blog
As forças fundamentais da Natureza
x
Borges e Nicolau
x
Exercícios básicos
Exercício 1: resolução
A força de atrito e a força normal resultam da interação entre partículas eletrizadas próximas. São, portanto, forças eletromagnéticas.
Resposta: c
x
Clique aqui para voltar ao Blog
quarta-feira, 9 de dezembro de 2020
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
λ = h/p => 780.10-9m= 6,63.10-34J.s/p => p = 8,5.10-28 J.s/m
Resposta: d
Clique aqui para voltar ao Blog
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
λ = h/p => 780.10-9m= 6,63.10-34J.s/p => p = 8,5.10-28 J.s/m
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
A) O comprimento de onda de De Broglie é dado por λ = h/p onde h é a constante de Planck, e p é o momentum da partícula.
B) Uma vez que o momentum é dado por mv, onde m indica a massa, e v, a velocidade da partícula, observamos que as partículas com mesma velocidade, mas massas diferentes, não podem ter o mesmo comprimento de onda de De Broglie.
Clique aqui para voltar ao Blog
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
A) O comprimento de onda de De Broglie é dado por λ = h/p onde h é a constante de Planck, e p é o momentum da partícula.
B) Uma vez que o momentum é dado por mv, onde m indica a massa, e v, a velocidade da partícula, observamos que as partículas com mesma velocidade, mas massas diferentes, não podem ter o mesmo comprimento de onda de De Broglie.
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
Os fenômenos apresentados nas alternativas a), b) e d) mostram que a luz se comporta como partícula na “colisão” com elétrons da matéria. A difração de elétrons evidencia o comportamento ondulatório de partículas subatômicas.
A propagação, no vácuo, de ondas de rádio não está relacionado com o dualismo onda-partícula.
Resposta: e
Clique aqui para voltar ao Blog
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
Os fenômenos apresentados nas alternativas a), b) e d) mostram que a luz se comporta como partícula na “colisão” com elétrons da matéria. A difração de elétrons evidencia o comportamento ondulatório de partículas subatômicas.
A propagação, no vácuo, de ondas de rádio não está relacionado com o dualismo onda-partícula.
Resposta: e
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
As naturezas corpuscular e ondulatória não são antagônicas mas, sim, complementares: é a complementaridade de Bohr.
Resposta: b
Clique aqui para voltar ao Blog
O caráter dual da luz
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
As naturezas corpuscular e ondulatória não são antagônicas mas, sim, complementares: é a complementaridade de Bohr.
Resposta: b
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
O comprimento de onda associado à bola de futebol é extremamente pequeno quando comparado com suas dimensões. Por isso, não podemos observar efeitos ondulatórios como, por exemplo, a difração. Lembre-se que a difração só será nítida se as dimensões da abertura ou do obstáculo forem da ordem de grandeza do comprimento de onda da onda incidente. O comprimento de onda associado ao elétron é da ordem do comprimento de onda dos raios X, realçando que sempre existem, associadas às partículas ao nível atômico, as propriedades das ondas.
Clique aqui para voltar ao Blog
O caráter dual da luz
Exercícios básicos
Borges e Nicolau
Exercício 4: resolução
O comprimento de onda associado à bola de futebol é extremamente pequeno quando comparado com suas dimensões. Por isso, não podemos observar efeitos ondulatórios como, por exemplo, a difração. Lembre-se que a difração só será nítida se as dimensões da abertura ou do obstáculo forem da ordem de grandeza do comprimento de onda da onda incidente. O comprimento de onda associado ao elétron é da ordem do comprimento de onda dos raios X, realçando que sempre existem, associadas às partículas ao nível atômico, as propriedades das ondas.
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
λ = h/(m.v) => λ = 6,63.10-34/(400.10-3.10) => λ ≅ 1,7.10-34 m
Resposta: λ ≅ 1,7.10-34 m
Clique aqui para voltar ao Blog
O caráter dual da luz
Exercícios básicos
Borges e Nicolau
Exercício 3: resolução
λ = h/(m.v) => λ = 6,63.10-34/(400.10-3.10) => λ ≅ 1,7.10-34 m
Resposta: λ ≅ 1,7.10-34 m
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
O caráter dual da luz
λ = h/(m.v) => λ = 6,63.10-34/(9,11.10-31.3,0.106) => λ ≅ 2,4.10-10 m
Resposta: λ ≅ 2,4.10-10 m
Clique aqui para voltar ao Blog
O caráter dual da luz
Exercícios básicos
Borges e Nicolau
Exercício 2: resolução
λ = h/(m.v) => λ = 6,63.10-34/(9,11.10-31.3,0.106) => λ ≅ 2,4.10-10 m
Resposta: λ ≅ 2,4.10-10 m
Clique aqui para voltar ao Blog
Cursos do Blog - Eletricidade
37ª aula
Efeito Fotoelétrico (II)
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Para que ocorra efeito fotoelétrico a energia transportada pelo fóton (E = h.f) deve ser maior do que a quantidade mínima de energia Φ (função trabalho) que um elétron necessita receber para ser extraído do metal. Portanto, para que haja emissão, deve-se aumentar a frequência da luz incidente.
Resposta: b
Clique aqui para voltar ao Blog
Efeito Fotoelétrico (II)
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Para que ocorra efeito fotoelétrico a energia transportada pelo fóton (E = h.f) deve ser maior do que a quantidade mínima de energia Φ (função trabalho) que um elétron necessita receber para ser extraído do metal. Portanto, para que haja emissão, deve-se aumentar a frequência da luz incidente.
Resposta: b
Clique aqui para voltar ao Blog
terça-feira, 8 de dezembro de 2020
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 5: resolução
f = v/4L => f = 340/4.2,5.10-2 => f = 3,4.103 Hz
Resposta: 3,4.103 Hz
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 4: resolução
fSol = (4/5).fSi => vSol/2L = (4/5).vSi/2L => vSol = (4/5).vSi =>
√(fSol/μ) = (4/5)√(fSi/μ) =>
fSol = (16/25).fSi
Resposta: b
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 3: resolução
fM = 2.fm => vM/2L = 2.vm/2L => vM = 2.vm =>
√(F/μM) = 2.√(F/μm) = μm/μM = 4
Resposta: b
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 2: resolução
A) Correta. A propagação do som não ocorre no vácuo, isto é, só ocorre em um meio material.
B) Correta. O maior comprimento de onda possível corresponde ao modo mais simples de a corda vibrar, isto é a um nó em cada extremidade e entre eles um único ventre.
Sendo L ao comprimento da corda, obtemos: L = λ/2 => λ = 2L
C) Correta. De v = √(F/μ) => v2 = F/(m/L) => v2 = F.L/m
D) Incorreta. No tubo sonoro fechado temos sempre um ventre na embocadura e um nó na outra extremidade. O modo mais simples de vibração é representado abaixo:
Temos: L = λ/4 => λ = 4L
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios de Revisão
Revisão/Ex 1: resolução
a) Com a corda vibrando no seu modo fundamental, temos dois nós nas extremidades e um ventre. Logo,
λ/2 = L => λ/2 = 0,35 m => λ = 0,70 m
v = λ.f => v = 0,7.680 => v = 476 m/s
b) A frequência fundamental da onda sonora é a frequência fundamental de vibração da corda.
v = λ.f => 340 = λ.680 => λ = 0,50 m
Respostas; a) 476 m/s b) 0,50 m
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39° aula
Cordas vibrantes / Tubos sonoros
Borges e Nicolau
Exercícios básicos
Exercício 6: resolução
Clique aqui para voltar ao Blog
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 6: resolução
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 5: resolução
Tubo aberto:
Tubo fechado:
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 4: resolução
λ/4 + λ/2 + λ/2 = L => λ = 4.L/5 e f = 5.v/4.L
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 3: resolução
λ/4 + λ/2 + λ/2 + λ/4 = L => λ = 2.L/3 e f = 3.v/2.L
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 2: resolução
a)
b)
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
39ª aula
Cordas vibrantes / Tubos sonoros
Exercícios básicos
Exercício 1: resolução
L = 3.λ/2; λ = 2.L/3; f = 3.(v/2L)
L = 4.λ/2; λ = 2.L/4; f = 4.(v/2L)
Clique aqui para voltar ao Blog
segunda-feira, 7 de dezembro de 2020
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 5: resolução
Tomando o ponto A como referência:
MPplaca + MPbarra = MT.senB => 200.8 + 100.4 = T.(6/10).8 =>
1600 + 400 = T.4,8 => T = 2000/4,8 => T = 416,66 N => T ≅ 417 N
Resposta: a
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 5: resolução
MPplaca + MPbarra = MT.senB => 200.8 + 100.4 = T.(6/10).8 =>
1600 + 400 = T.4,8 => T = 2000/4,8 => T = 416,66 N => T ≅ 417 N
Resposta: a
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
A máxima distância que o jovem pode percorrer, medida a partir de B, sem que a prancha gire, corresponde ao instante em que a força normal em A torna-se nula.
Nestas condições, tomando o ponto B como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Pprancha x 1,5 = Pjovem x d => 900 x 1,5 = 600 x d => d = 2,25 m
Resposta: c
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
A máxima distância que o jovem pode percorrer, medida a partir de B, sem que a prancha gire, corresponde ao instante em que a força normal em A torna-se nula.
Nestas condições, tomando o ponto B como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Pprancha x 1,5 = Pjovem x d => 900 x 1,5 = 600 x d => d = 2,25 m
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
mB.g.30 = mA.g.10 => mB = mA/3 = 15 gramas.
T = mA.g + mB.g = 60.g
T.20 = mC.g.30 => 60.g.20 = mC.g.30 => mC = 40 gramas
Resposta: d
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
mB.g.30 = mA.g.10 => mB = mA/3 = 15 gramas.
T = mA.g + mB.g = 60.g
T.20 = mC.g.30 => 60.g.20 = mC.g.30 => mC = 40 gramas
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
Tomando a articulação como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Mg.L + mg.(L/2) = Kx.(L/2) => x = (2M+m).g/K
Resposta: d
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 2: resolução
Tomando a articulação como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Mg.L + mg.(L/2) = Kx.(L/2) => x = (2M+m).g/K
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Tomando o ponto P como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Phaste.(L/2) + Mg.2L = M’g.L => M’ = 2M + Phaste/2g
Portanto, M’ > 2M
Resposta: d
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 1: resolução
Tomando o ponto P como referência e considerando que a soma dos momentos das forças que tendem a produzir rotação no sentido horário é igual à soma dos momentos das forças que tendem a produzir rotação no sentido anti-horário, temos:
Phaste.(L/2) + Mg.2L = M’g.L => M’ = 2M + Phaste/2g
Portanto, M’ > 2M
Resposta: d
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 5: resolução
Condições de equilíbrio:
1ª) YA + T.sen 30º = P + PB => YA + T.(1/2) = 30 + 10 (1)
XA = T.cos 30º => XA = T.(√3/2) (2)
2ª) Tomando o ponto A como referência:
MP + MPB = MTsen30º => 30.3 + 10.6 = T.(1/2).4 => T = 75 N
De (1): YA = 2,5 N
De (2): XA = 37,5.√3 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 5: resolução
Condições de equilíbrio:
1ª) YA + T.sen 30º = P + PB => YA + T.(1/2) = 30 + 10 (1)
XA = T.cos 30º => XA = T.(√3/2) (2)
2ª) Tomando o ponto A como referência:
MP + MPB = MTsen30º => 30.3 + 10.6 = T.(1/2).4 => T = 75 N
De (1): YA = 2,5 N
De (2): XA = 37,5.√3 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
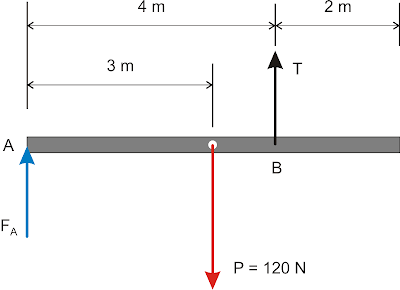
Exercício 4: resolução
Condições de equilíbrio:
1ª ) FA + T = P => FA + T = 120 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 120.3 = T.4 => T = 90 N
Mas o peso do bloco é igual à intensidade da força de tração no fio, isto é:
P = T = 90 N
De (1): FA = 30 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 4: resolução
Condições de equilíbrio:
1ª ) FA + T = P => FA + T = 120 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 120.3 = T.4 => T = 90 N
Mas o peso do bloco é igual à intensidade da força de tração no fio, isto é:
P = T = 90 N
De (1): FA = 30 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 3: resolução
Tomando o ponto O como referência:
MPJ = MPM => 500.2 = PM.4 => PM = 250 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 3: resolução
Tomando o ponto O como referência:
MPJ = MPM => 500.2 = PM.4 => PM = 250 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 2: resolução
a)
b) Condições de equilíbrio:
1ª) FA + T = P => FA + T = 90 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 90.2 = T.4 => T = 45 N
De (1): FA = 45 N
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 2: resolução
a)
b) Condições de equilíbrio:
1ª) FA + T = P => FA + T = 90 (1)
2ª) Tomando o ponto A como referência:
MP = MT => 90.2 = T.4 => T = 45 N
De (1): FA = 45 N
Clique aqui para voltar ao Blog
Cursos do Blog - Mecânica
39ª aula
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 1: resolução
a) MF = F.d = 10 N.2 m = 20 N.m
b) MFA = 0, pois a distância de A à linha de ação de fA é zero.
Clique aqui para voltar ao Blog
Equilíbrio Estático de um corpo extenso
Borges e Nicolau
Exercícios básicos
Exercício 1: resolução
a) MF = F.d = 10 N.2 m = 20 N.m
b) MFA = 0, pois a distância de A à linha de ação de fA é zero.
Clique aqui para voltar ao Blog
terça-feira, 1 de dezembro de 2020
Cursos do Blog - Termologia, Óptica e Ondas
37ª aula
Reflexão e Refração de Ondas
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 5: resolução
Da figura tiramos: 1,5.λ1 = 6 => λ1 = 4 m
Sendo v2/v1 = λ2/λ1, vem: 10/8 = λ2/4 => λ2 = 5 m
Resposta: c
Clique aqui para voltar ao Blog
Reflexão e Refração de Ondas
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 5: resolução
Da figura tiramos: 1,5.λ1 = 6 => λ1 = 4 m
Sendo v2/v1 = λ2/λ1, vem: 10/8 = λ2/4 => λ2 = 5 m
Resposta: c
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
37ª aula
Reflexão e Refração de Ondas
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
Na corda PQ, temos:
v1 = λ1.f => 15 = 1,5.f => f = 10 Hz
A frequência de vibração da corda é a mesma da fonte:
ffonte = 10 Hz
Na refração a frequência não se altera. Assim, temos:
v2 = λ2.f => 6 = λ2.10 => λ2 = 0,6 m
Respostas: 10 Hz e 0,6 m
Clique aqui para voltar ao Blog
Reflexão e Refração de Ondas
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 4: resolução
Na corda PQ, temos:
v1 = λ1.f => 15 = 1,5.f => f = 10 Hz
A frequência de vibração da corda é a mesma da fonte:
ffonte = 10 Hz
Na refração a frequência não se altera. Assim, temos:
v2 = λ2.f => 6 = λ2.10 => λ2 = 0,6 m
Respostas: 10 Hz e 0,6 m
Clique aqui para voltar ao Blog
Cursos do Blog - Termologia, Óptica e Ondas
37ª aula
Reflexão e Refração de Ondas
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
Se a extremidade for livre o pulso reflete sem inversão, conforme a figura:
Se a extremidade for fixa o pulso reflete invertido, conforme a figura:
Resposta: a
Clique aqui para voltar ao Blog
Reflexão e Refração de Ondas
Borges e Nicolau
Exercícios de Revisão
Revisão/Ex 3: resolução
Se a extremidade for livre o pulso reflete sem inversão, conforme a figura:
Se a extremidade for fixa o pulso reflete invertido, conforme a figura:
Resposta: a
Clique aqui para voltar ao Blog
Assinar:
Comentários (Atom)